This problem comes from LeetCode: https://leetcode.com/problems/reshape-the-matrix, “Reshape the Matrix”.
You are given an
m x nmatrixmatand two integersrandcrepresenting the number of rows and the number of columns of the wanted reshaped matrix.The reshaped matrix should be filled with all the elements of the original matrix in the same row-traversing order as they were.
If the
LeetCode problem 566reshapeoperation with given parameters is possible and legal, output the new reshaped matrix; Otherwise, output the original matrix.
Honestly whenever I hear the word matrix, I think of very complicated things maybe because of the movie The Matrix, but this matrix is simply a table that consist of rows and columns, so there is nothing fancy about it. I will solve this in C#.
In our problem we have already a matrix that looks something like this:
Before we start doing anything, just take a moment and see that
We have two rows:
Row one: 1, 2
Row two: 3, 4
We have two columns:
Column one: 1, 3
Column two: 2, 4
Input is like this = [[1,2],[3,4]], which is actually easier to read like this:
[[1,2],
[3,4]]
From our initial matrix we want to be able to reshape it to look something like this if we pass the parameters:
r = 1 and c = 4.
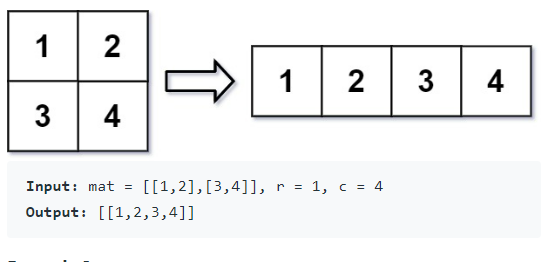
Check if we can actually reshape the matrix to our desired shape
First we want to check if it is possible to reshape it to a new matrix, if it is legal, that is to say, we have enough rows and columns to fit. To do that we can check how our new matrix would look like with the assigned rows and columns length. By comparing number of rows (parameter r) * number of columns (parameter c) with the length of the current matrix we want to reshape which we can get the rows from by checking the matrix overall length with a rows length (because every row is of the same length, that is to say, each row contains the same amount of columns).
// Cant reshape, size doesnt match
if(r * c != (mat.Length * mat[0].Length)) {
return mat;
}Initiate a new matrix 2D array.
Now let’s initialize our new matrix, it will be of the same type that came in, that is int[][]. We already know how it should look, it should have r amount of rows, and c amount of columns. Now we can’t do this as much as we wish we could, because each array must be initalized on its own.
int[][] newMat = new int[r][c];Instead, we can initalize the array like this:
int[][] newMat = new int[r][];
// Set column size for each row
for(int x = 0; x < newMat.Length; x++) {
newMat[x] = new int[c];
}First we set the size of the array. And for each row, we set the row-element to hold another array that have size of c. Thus we have defined our new matrix array with the right size.
Set values to the matrix
Now to the fun part, we can set the values from our old matrix to our new matrix. We can loop through it and set its values depending on if we are done filling our row and columns. To keep track of this, we need some variables, and one way to do this, is to set which row and column we are at while we are looping through the original matrix.
Help variables
int row_number = 0;
int column_number = 0;Then we utilize this when going through the rows and columns, we start at row 0 and column 0.
Traverse through the matrix and fetch and set values
// Go through rows
for(int i = 0; i < mat.Length; i++) {
// Go through columns
for(int j = 0; j < mat[0].Length; j++) {
newMat[row_number][column_number] = mat[i][j];
column_number++;
// If we reached desired column length
if(column_number == c) {
// Go back to column one
column_number = 0;
row_number++;
}
}
}In the for loop we get the value from the matrix. When we are done, we increment the column_number, so we are at the next column position at the next time we fetch the value from the matrix from the next column, and each time we check if we reached the end of the column length, if so, reset the column back 0, and increment the row so that we start at the next row, and continue fetching values. We can never go out of index because our first check in the program to see if we have enough rows and columns for all the values for the matrix, so we don’t need an actual row check, we can just keep on incrementing.
When we are done going through all the values, we return the new matrix:
return newMat;
The whole code looks like this in the end:
public class Solution {
public int[][] MatrixReshape(int[][] mat, int r, int c) {
// Cant reshape, size doesnt match
if(r * c != (mat.Length * mat[0].Length)) {
return mat;
}
int[][] newMat = new int[r][];
// Set column size for each row
for(int x = 0; x < newMat.Length; x++) {
newMat[x] = new int[c];
}
int row_number = 0;
int column_number = 0;
// Go through rows
for(int i = 0; i < mat.Length; i++) {
// Go through columns
for(int j = 0; j < mat[0].Length; j++) {
newMat[row_number][column_number] = mat[i][j];
// Next column
column_number++;
// If we reached desired column length
if(column_number == c) {
// Go back to column one
column_number = 0;
// Go to next row
row_number++;
}
}
}
return newMat;
}
}Time complexity: O(m * n)
Since we know that it is said that in MATLAB, there is a function called reshape which can reshape an m x n matrix[…] we know that the original matrix consist of the variables m * n and the m is the rows and the n stands for columns, and what our functions does, is that it goes through the rows, and all the rows columns one time only, meaning that we will have a time complexity of O(m * n).
